Chapter 15 | Statistics and Probability | Class-8 DAV Secondary Mathematics

Are you looking for DAV Maths Solutions for class 8 then you are in right place, we have discussed the solution of the Secondary Mathematics book which is followed in all DAV School. Solutions are given below with proper Explanation please bookmark our website for further updates!! All the Best !!

Chapter 15 | Statistics and Probability | Class-8 DAV Secondary Mathematics

Unit 15 Worksheet 1 || Statistics and Probability

1. Given below are the ages of 30 students of Class-VIII in a school.

13 14 14 12 15 15 14 13 13 14 14 15 13 14 14 12 14 13 12 13 14 14 13 12 13 12 13 14 15 14 . Prepare a frequency distribution table.

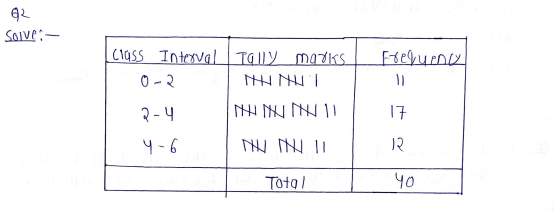
2. The following data gives the number of children in 40 families:

1 2 6 5 I 5 1 3 2 6 2 3 4 2 0 4 4 3 2 2 0 0 I 2 2 4 3 2 I 0 5 1 2 4 3 4 1 6 2 2. Represent it in the form of a frequency distribution table.

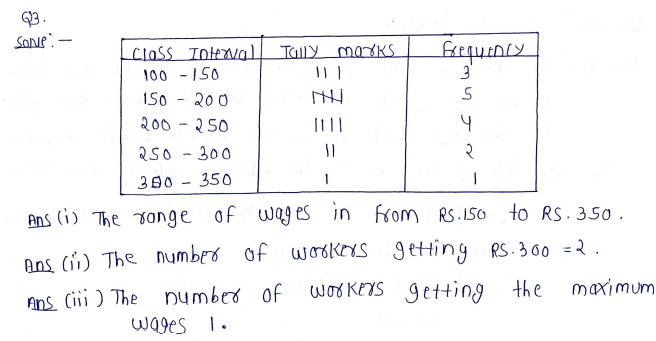
3. The daily wages (in Rs.) of 15 workers in a factory arc the following: 300 250 200 250 200 250 200 150 350 200 150 300 150 200 250

Prepare a frequency distribution table.

(i) What is the range of wages (in Rs.?)?

(ii) How many workers are getting Rs.300?

(iii) How many workers are getting the maximum wages?

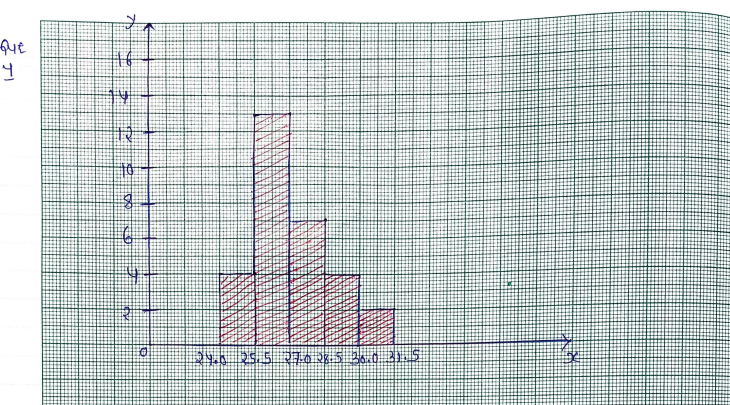
4. The daily minimum temperature (in °C) in Delhi for the 30 days of June in a particular year was as under
27.1 26.3 30.4 29.5 29.3 30.1 30.0 26.5 27.0 27.1 28.0 28.6 27.9 27.0 26.9 26.8 25.3 25.5 24.9 26.4 26.9 26.8 27.3 27.5 25.8 25.9 25.5 26.4 26.6 27.5

Prepare a frequency table taking class intervals 24.0-25.5, 25.5-27.0 etc. Also prepare a histogram. Find the class interval, class size and class mark corresponding to the maximum frequency.

5. Read the following histogram and answer the questions given after it.

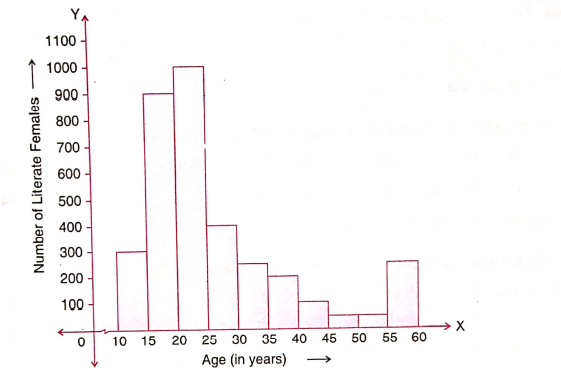
(i) What information is depicted by the above histogram?

(ii) In which age group is the number of literate females maximum?

(iii) In which age group is the number of literate females minimum?

(iv) How many females below 35 years of age are literate?

6. Given below is the histogram depicting the marks obtained by 40 students of Class-VIII in a test of English. Look at it carefully and answer the questions that follow:

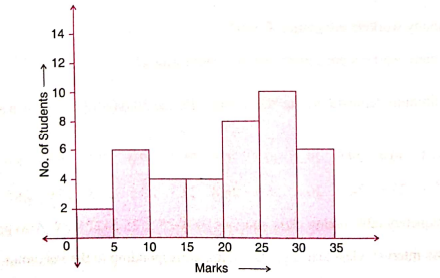
(i) What is the class size?

(ii) How many students obtained less than 10 marks?

(iii) How many students obtained 15 or more but less than 30 marks?

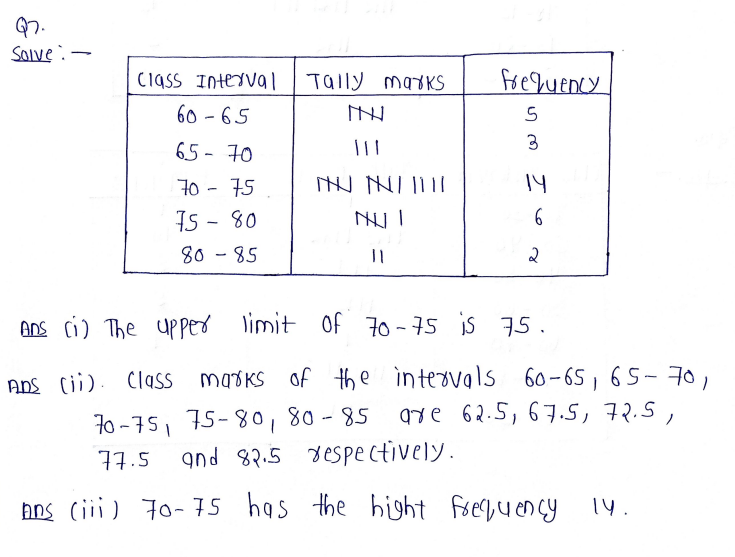
7. The pulse rate (per minute) of 30 persons was recorded as

61 76 72 73 71 66 78 73 68 81 78 63 72 75 80 68 75 62 71 81 73 60 79 72 73 74 71 64 76 71 Construct a frequency table using class intervals 60 — 65, 65 — 70, etc.

(i) What is the upper limit of third class interval?

(ii) What are the class marks of each class interval?

(iii) Which class interval has the highest frequency?

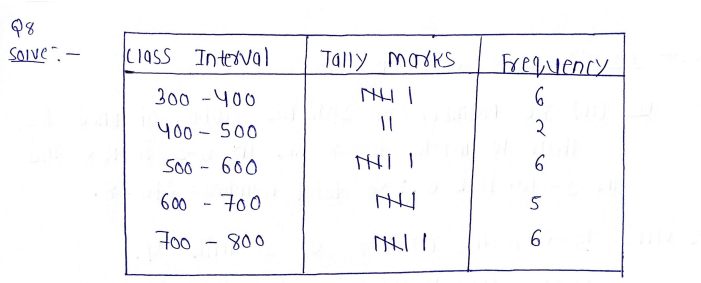
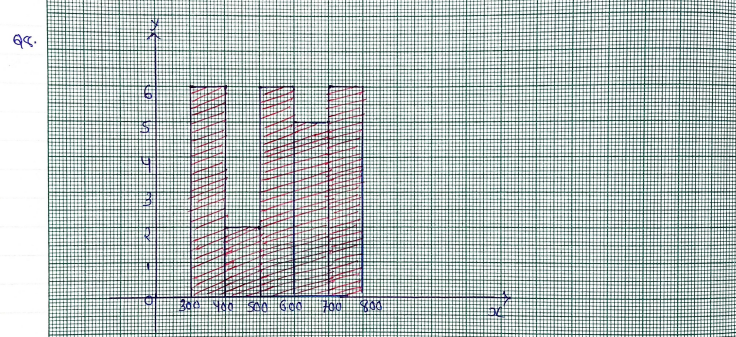
8. The electricity bills (in rupees) of 25 houses of a certain locality for a month are given below:

324 700 617 400 356 365 435 506 548 736 780 378 570 685 312 630 584 674 754 776 596 745 565 763 472. Prepare a frequency table taking class intervals 300-400, 400-500, etc. Also prepare a histogram.

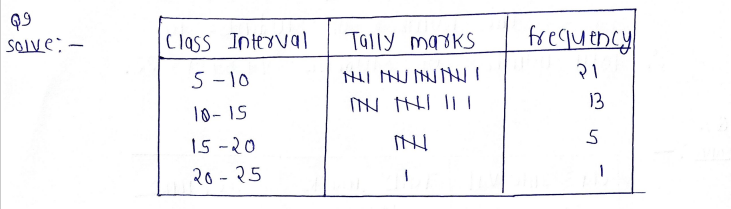
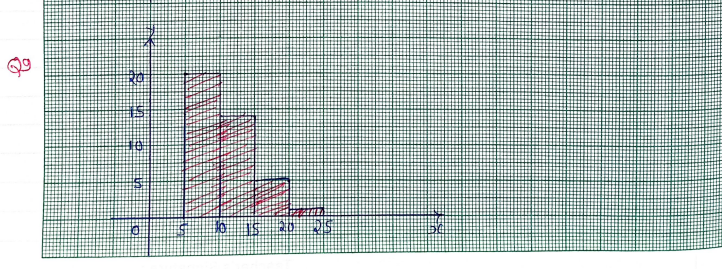
9. There are 40 students in a class. Their ages are as follows. Construct a frequency distribution table with one of the class intervals 5-10. Draw histogram also.
13 21 6 5 8 17 14 13 6 6 7 8 15 16 9 10 10 9 7 8 15 14 12 II 9 7 6 8 6 10 13 17 17 16 12 12 9 8 13 14

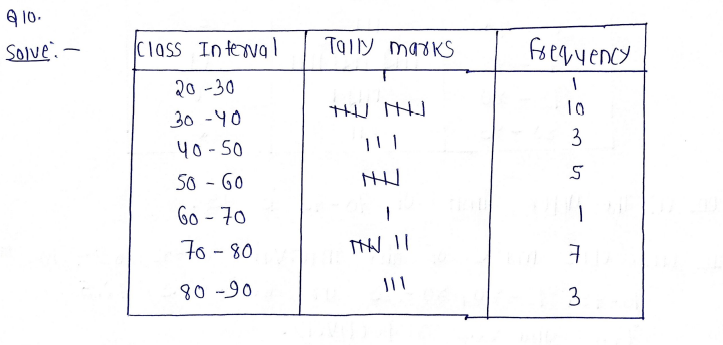
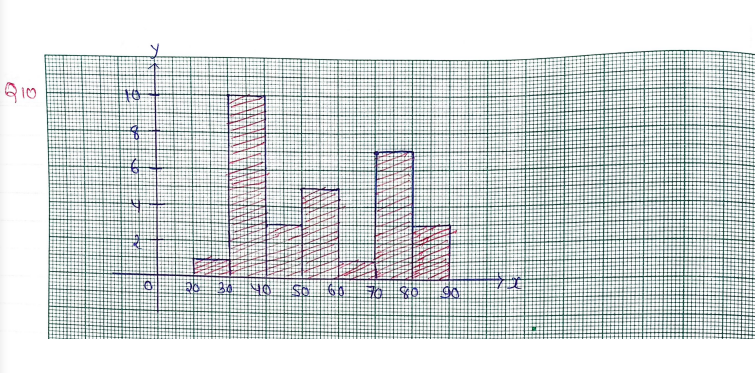
10. Yearly savings (in rupees) of 30 students of Class-VII are given below. Prepare a frequency distribution table with one of the class intervals 30 — 40. Also prepare a histogram.
38 42 40 35 72 27 57 82 59 80 84 73 65 40 76 40 38 60 58 38 54 39 50 44 71 83 45 38 80 77