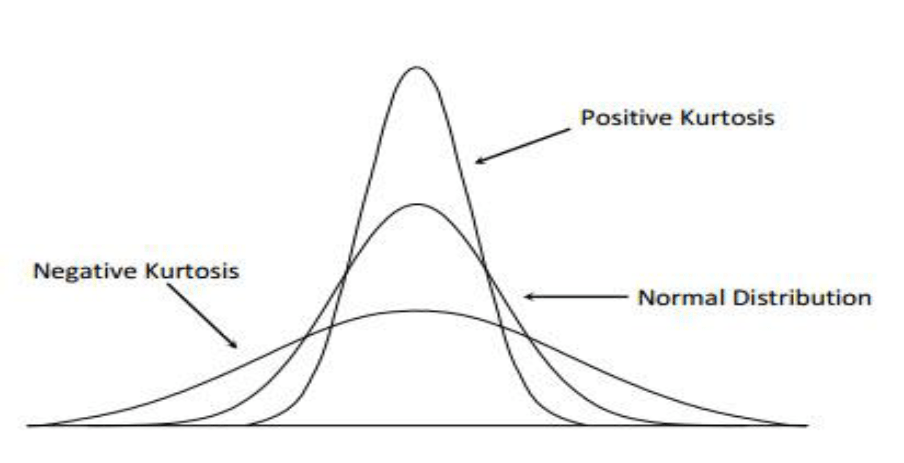
Kurtosis enables us to have an idea about the ‘flatness or peakedness’ of the frequency curve. It is a measure of the “tailedness” of the probability distribution
1. Mesokurtic
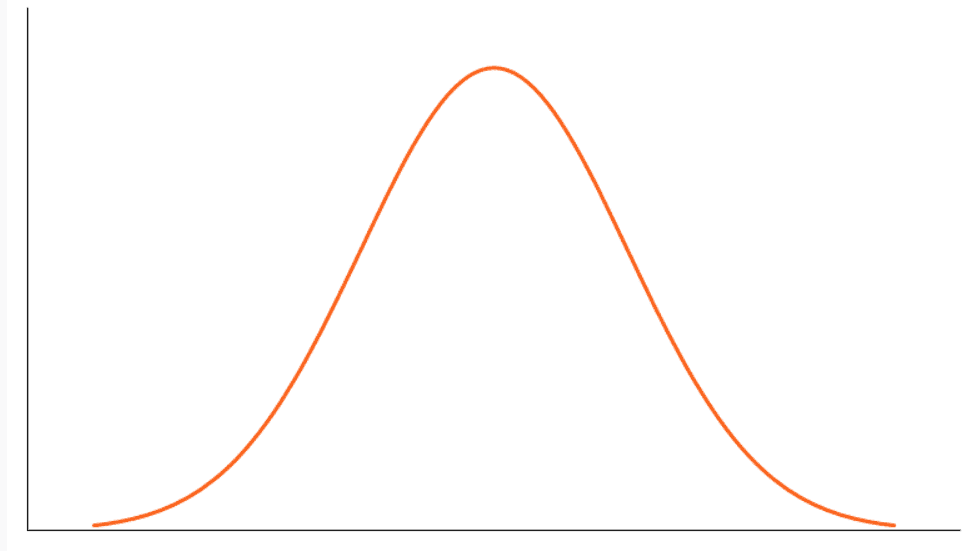
Curve which is neither flat nor peaked is called the normal or mesokurtic curve; for such a curve β2 = 3, and 𝛾2 = 0. Data that follows a mesokurtic distribution shows an excess kurtosis of zero or close to zero. This means that if the data follows a normal distribution, it follows a mesokurtic distribution.
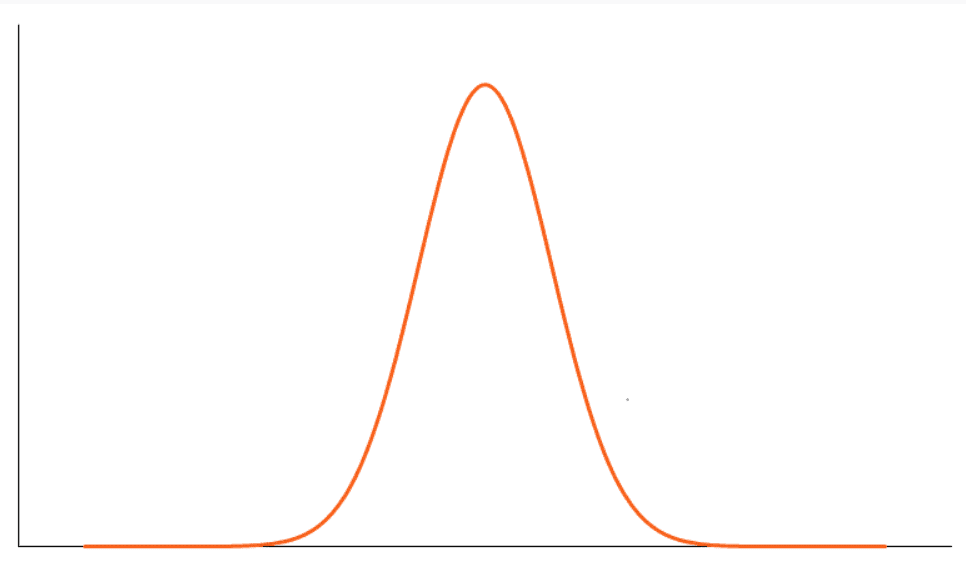
2. Leptokurtic
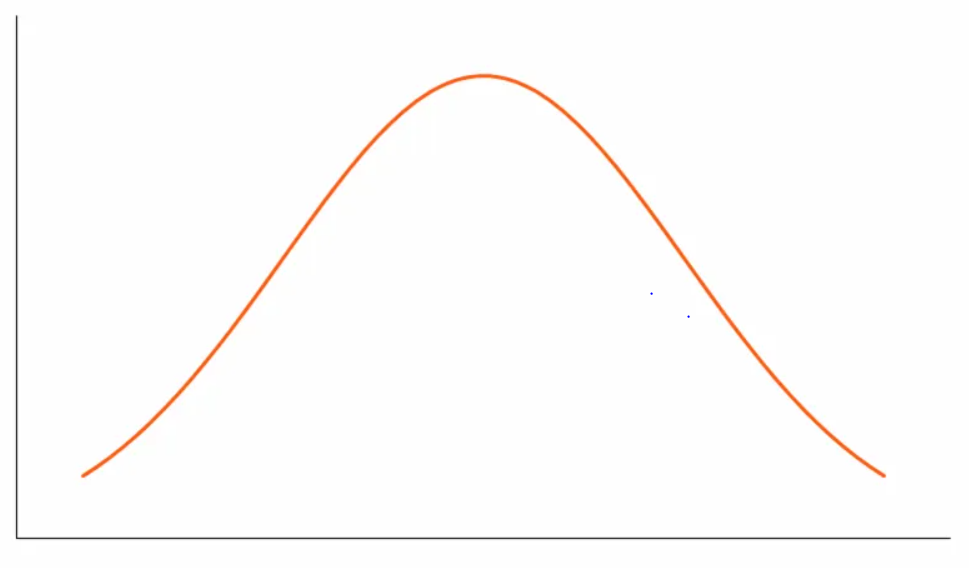
Curve which is flatter than the normal curve is known as platykurtic; for such a curve β2 < 3 and 𝛾2 < 0; they are said to have negative kurtosis.
3. Platykurtic
Curve which is more peaked than the normal curve is called leplokurtic; for such a curve β2 > 3 and 𝛾2 > 0; they are said to have positive kurtosis.
What is Excess Kurtosis?
An excess kurtosis is a metric that compares the kurtosis of a distribution against the kurtosis of a normal distribution. The kurtosis of a normal distribution equals 3. Therefore, the excess kurtosis is found using the formula below:
Excess Kurtosis = Kurtosis – 3