NCERT Class 9 Maths Solutions PDF: In this post, we have discussed the solution of the Maths class 9 book which is followed in all CBSE schools. Solutions are given below with proper Explanation and utmost care has been taken to ensure that the solutions are correct. Answers provided will not only help in completing all the assignments but also help students in clearing their concepts. Students can download the solutions by printing the chapters by using the command Ctrl+P in google chrome and saving it in PDF format. All the best !! Please support us by sharing this website with your school friends.
Exercise 10.5 Class 9 Maths Chapter 10 Circles
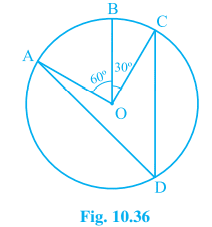
1. In Fig. 10.36, A,B and C are three points on a circle with centre O such that ∠ BOC = 30° and ∠AOB = 60°. If D is a point on the circle other than the arc ABC, find ∠ADC.
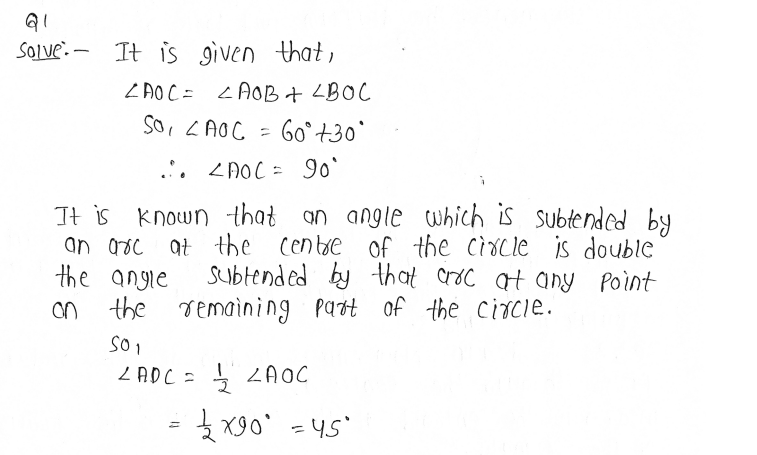
2. A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.

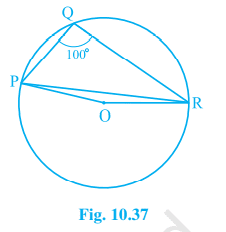
3. In Fig. 10.37, ∠ PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠ OPR.

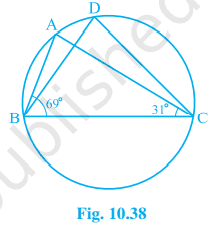
4. In Fig. 10.38, ∠ ABC = 69°, ∠ ACB = 31°, find ∠ BDC.
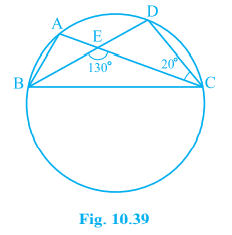
5. In Fig. 10.39, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠ BEC = 130° and ∠ ECD = 20°. Find ∠ BAC.
6. ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠ DBC = 70°, ∠ BAC is 30°, find ∠ BCD. Further, if AB = BC, find ∠ ECD.

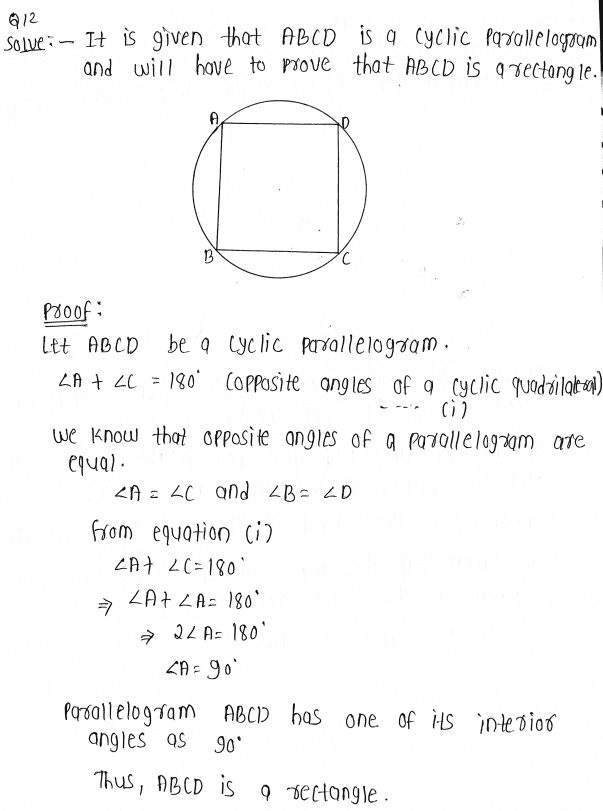
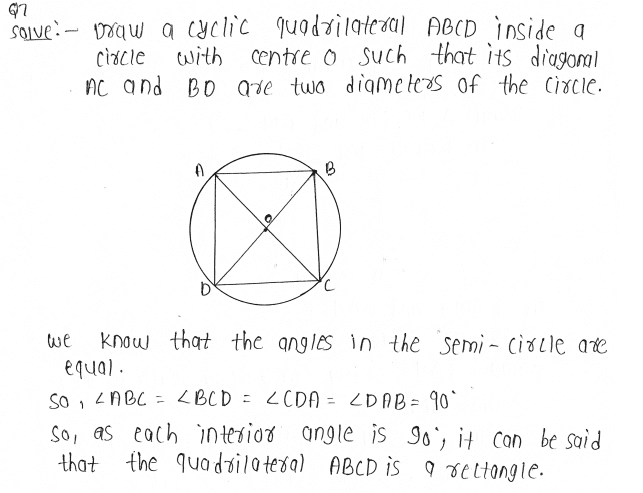
7. If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
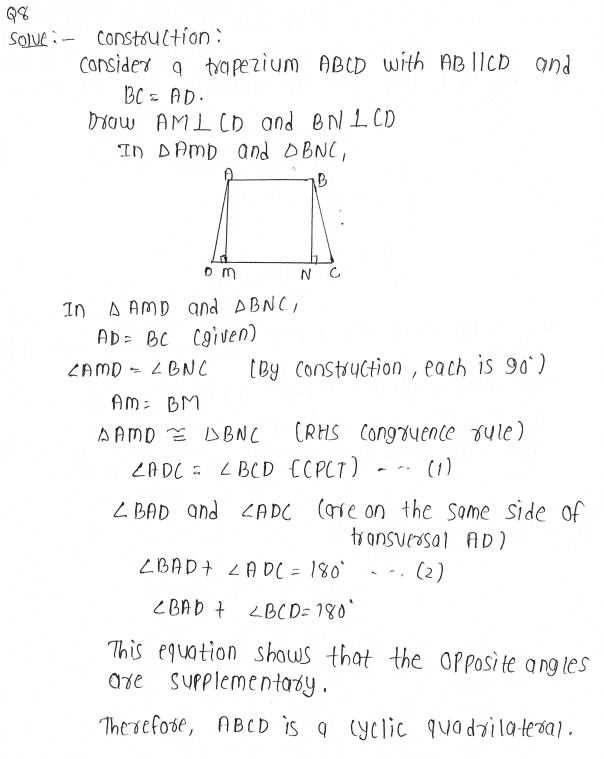
8. If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
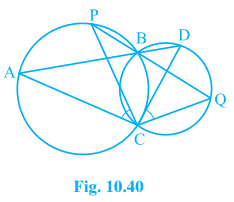
9. Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see Fig. 10.40). Prove that ∠ACP = ∠QCD.

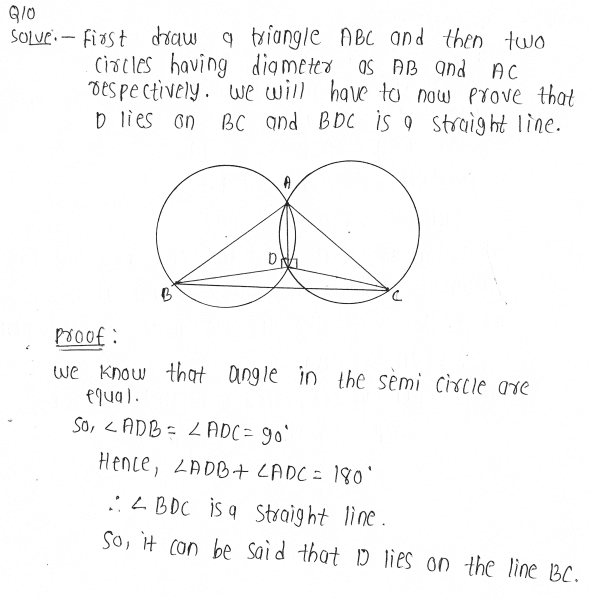
10. If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
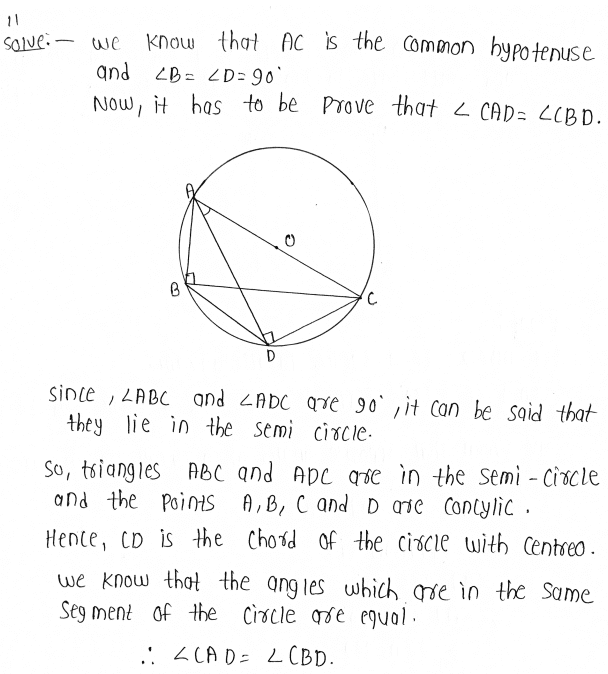
11. ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠ CAD = ∠CBD.
12. Prove that a cyclic parallelogram is a rectangle.