Are you looking for DAV Maths Solutions for class 8 then you are in right place, we have discussed the solution of the Secondary Mathematics book which is followed in all DAV School. Solutions are given below with proper Explanation please bookmark our website for the further update !! All the Best !!
DAV SOLUTIONS CLASS 8 Secondary Mathematics Unit 1 Worksheet 1
Question 1 : Which of the following numbers are perfect squares? 11, 16, 32, 36, 50, 64, 75
Answer: 16,36 and 64 are Perfect Squares .
Explanation: As 16 can be written as 4*4 , 36 can be expressed as 36=6*6, 64 can be expressed as 64=8*8 therefore 16,36 and 64 are Perfect Squares .
Question 2:Which of the following numbers are perfect squares of even numbers? 121, 225, 784, 841, 576, 6561
Answer: 576 and 784 are perfect square
Explanation: Perfect Square of Even Number is always even as Even*Even is also a Even number, therefore 121,225,841 and 6561 are eliminated. Prime factorization of 576 is 26 × 32 therefore finding the Square root we get=23*31 =24 which is an even number. Similarly, The Prime Factorization of 784 is 24 × 7 finding the Square root we get =22 *7=28 which is an even number.
Question 3: Which of the following numbers are perfect squares? 100, 205000, 3610000, 212300000
Answer: 100,3610000 are a perfect square.
Explanation: Prime factors of 100: 2×2, 5×5 Finding pairs we get=2*5=10 therefore 100 is Square of 10 we can say that 100 is a perfect square. ,
Prime factors of 20500 : 2×2, 5x5x5, 41 Since there are no pair of 41, 20500 is not a perfect Square,
Prime factors of 3610000: 2x2x2x2, 5x5x5x5, 19×19 , here all prime numbers are in pair,3610000=1900*1900 therefore 3610000 is a perfect square,
Prime factors of 212300000: 2x2x2x2x2, 5x5x5x5x5, 11, 193 no pair of 193 is available in prime factorization so 21300000 is not a perfect square.
Question 4:By just observing the digits at one’s place, tell which of the following can be perfect squares? 1026, 1022, 1024, 1027
Answer: We know that no square number ends in 2, 3, 7 or 8. we can easily infer that 1022 and 1027 can never be a perfect square.
Question 5: How many non-square numbers lie between the following pairs of numbers?
(i) 7^2 and 8^2 (ii) 10^2 and 11^2 (iv) 80^2 and 81^2 (v) 101^2 and 102^2
(iii) 40^2 and 41^2 (vi) 205^2 and 206^2
Answer: There are 2n natural numbers lying between two consecutive perfect square numbers n^2 and (n+1)^2
i. Here n=7 so there are 27=14 natural number between 7^2 and 8^2
ii, Here n= 10 so there are 210=20 natural number 10^2 and 11^2
iii, Here n=40 so there are 240=80 natural number 40^2 and 41^2
iv, Here n= 80 so there are 280=160 natural number 80^2 and 81^2
v, Here n= 101 so there are 2101=202 natural number 101^2 and 102^2
vi. Here n= 205 so there are 2205=410 natural number 205^2 and 206^2
Question 6 :Write down correct number in the box:
i. 1002 – 992 =(100-99)(100+99)=199
i. 272 – 262 =(27-26)(27+26)=53
i. 5692 – 5682 =(100-99)(100+99)=199
Answer: In general, then, the rule is: y squared minus x squared equals the difference between y and x multiplied by the sum of y and x. Algebraically, we can write this as: y2 – x2 = (y – x) x (y + x)=(y – x) (y + x)——Equation 1
Let us assume that y and x are consecutive number,difference between consecutive numbers is 1 so above equation reduces to y+x.
i.1002 – 992 =(100-99)(100+99)=199
ii. 272 – 262 =(27-26)(27+26)=53
iii.5692 – 5682 =(569-568)(569+568)=1137
Question 7 :Observe the following pattern in the following and find the missing numbers:
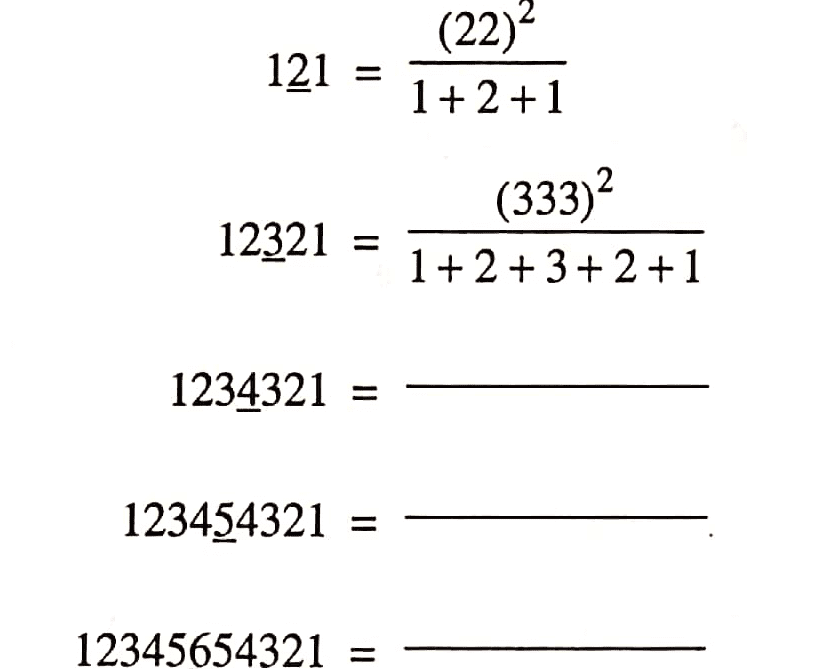
Answer: As per the pattern digit in the middle of number is written same times to form a number .In first case 2 is written as 22 ,resultant number is squared and divided by sum of digits.
1234321=44442 / 1+2+3+4+3+2+1
123454321=555552 / 1+2+3+4+5+4+3+2+1
12345654321=6666662 / 1+2+3+4+5+6+5+4+3+2+1
Question 8 :Observe the following pattern and fill in the blanks.
1+3 =22
1+3+5 =32
1+3+5+7 =42
1+3+5+7+9=
1+3+5+7+9+11=
1+3+5+7+9+11—–n =
Answer:
Sum of first n consecutive odd digit number is n2
1+3+5+7+9=52 =25
1+3+5+7+9+11=62 =36
1+3+5+7+9+11—–n =n2
Question 9 : Which of the following triplets are Pythagorean? (3, 4, 5), (6, 7, 8), (10, 24, 26), (2, 3, 4)
[Hint: Let the smallest even number be 2m and find in from it. Then, find (2m, m2 — 1, m2 + 1). If you get the triplet, it is Pythagorean.]
Another way of finding a Pythagorean triplet is: If ‘a’, ‘b and ‘c’ are three natural numbers with ‘a’ as the smallest of them, then
(i) If ‘a’ is odd, sum of other two numbers is a2 and their difference is 1.
(ii) If ‘a’ is even, sum of other two numbers is a2/2 and their difference is 2.
Answer: (3, 4, 5) Let 2m=4 , m=4/2=2 Now m2 -1 =22 -1=3 and m2 + 1 =22 +1=5
∴(3, 4, 5) is Pythagorean triplets.
(iii)Taking Triplets (6, 7, 8),Smallest Number=6 2m=6 m=3
Pythagorean triplets are 2m,m2 -1,m2 + 1 and its value are 6,8,10. Hence (6, 7, 8) is not a pythagorean triplets.
(iv)Taking Triplets (10, 24, 26),Smallest Number=10 2m=10 m=5
Pythagorean triplets are 2m,m2 -1,m2 + 1 and its value are 10,24,26. Hence (10, 24, 26) is a pythagorean triplets.
(v) Taking Triplets (2, 3, 4),Smallest Number=2 2m=2 m=1
Pythagorean triplets are 2m,m2 -1,m2 + 1 and its value are 2,0,2. Hence (2, 3, 4) is a not a pythagorean triplets.
- DAV class 8 Maths Book Solutions
- Chapter 1 | Square and Square Roots | Class-8 DAV Secondary Mathematics
- Chapter 2 | Cube and Cube Roots | Class-8 DAV Secondary Mathematics
- Chapter 3 | Exponents And Radicals | Class-8 DAV Secondary Mathematics
- Chapter 4 | Direct And Inverse Variation | Class-8 DAV Secondary Mathematics
- Chapter 5 | Profit, Loss And Discount | Class-8 DAV Secondary Mathematics
- Chapter 6 | Compound Interest | Class-8 DAV Secondary Mathematics
- Chapter 7 | Algebraic Identities | Class-8 DAV Secondary Mathematics
- Chapter 8 | Polynomials | Class-8 DAV Secondary Mathematics
- Chapter 9 | Linear Equations In One Variable | Class-8 DAV Secondary Mathematics
- Chapter 10 | Parallel Lines | Class-8 DAV Secondary Mathematics
- Chapter 11 | Understanding Quadrilaterals | Class-8 DAV Secondary Mathematics
- Chapter 12 | Construction Of Quadrilaterals | Class-8 DAV Secondary Mathematics
- Chapter 13 | Introduction To Graphs | Class-8 DAV Secondary Mathematics
- Chapter 14 | Mensuration | Class-8 DAV Secondary Mathematics
- Chapter 15 | Statistics and Probability | Class-8 DAV Secondary Mathematics
- Chapter 16 | Rotational Symmetry | Class-8 DAV Secondary Mathematics
Very nice
there is not worksheet 4 and worksheet 5 and brain treaser so please provide it to us.
Sorry! Will try to update today or by tomorrow.
Book