A geometric sequence is a type of sequence where every term except the first term is generated by multiplying the previous term by a fixed nonzero number called common ratio, r.
The formula for geometric series consists of:
Formula to find the nth term of a geometric series.
Finding the sum of a finite geometric series.
Finding the sum of an infinite geometric series.
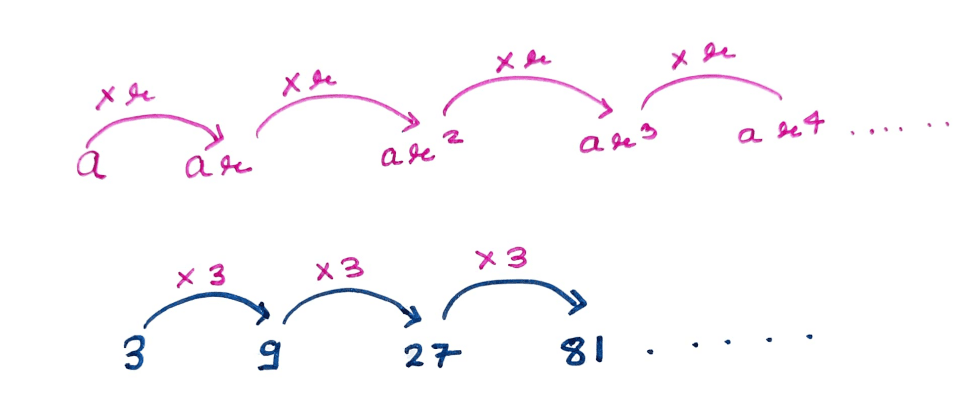
Important Facts about Geometric Series:
If we divide any term except first term by previous term then the quotient is same i.e. Constant r.
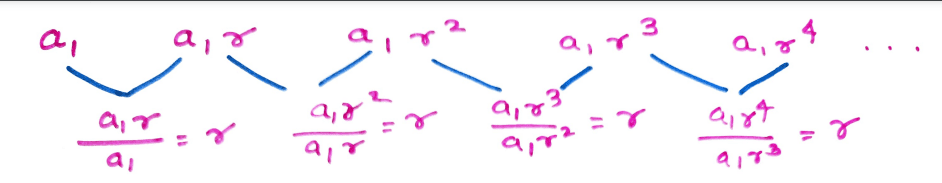
Let’s see Formula to find the nth term of a geometric series.
Writing the first term is the initial step in creating a geometric sequence. The second term of the geometric sequence is obtained by multiplying the first term by a constant nonzero value ie. r.
We multiply the second term by the common ratio to produce the third sequence. We can observe a pattern. The preceding phrase is multiplied by the constant nonzero number we used as the common multiplier to arrive to the next term in the sequence.
Let’s Understand using an example, we have a geometric sequence where
the first term, a1 is 7
and
the fixed constant or common ratio, r, is 3.
then the second term is obtained by multiplying it with fixed constant 3
The third term is generated by multiplying the second term by the fixed constant 3.
The fourth term is obtained by multiplying the third term by the fixed constant 3.
Observe that the first term a1 is always present in every term of the sequence. In the same manner, the fixed constant r is also attached in every term to some power. Notice that
- if n is 1 then the power of r is 0
- if n is 2 the power of r is 1
- if n is 3 the power of r is 2
- if n is 4 the power of r is 3
- if n is 5 the power of r is 4
Therefore, we can now deduce that the nth term an of a geometrc sequence is equal to the first term a1 multiplied to the fixed constant (also known as the common ratio) r raised to 1 less than n.
Therefore nth term of a geometric sequence is given by an = arn – 1