KSEEB Class 10 Maths Solutions Chapter 1 Arithmetic Progressions Ex 1.1

KSEEB SSLC Class 10 Maths Solutions Chapter 1 Arithmetic Progressions Ex 1.1 are part of KSEEB SSLC Class 10 Maths Solutions. Here we have given Karnataka SSLC Class 10 Maths Solutions Chapter 1 Arithmetic Progressions Exercise 1.1.

Karnataka SSLC Class 10 Maths Solutions Chapter 1 Arithmetic Progressions Exercise 1.1

Question 1.
In which of the following situations, does the list of numbers involved make an arithmetic progression, and why?

i) The taxi fare after each km when the fare is Rs. 15 for the first km and Rs. 8 for each additional km.

ii) The amount of air present in a cylinder when a vacuum pump removes of the air remaining in the cylinder at a time.

iii) The cost of digging a well after every metre of digging when it costs Rs. 150 for the first metre and rises by Rs. 50 for each subsequent metre.

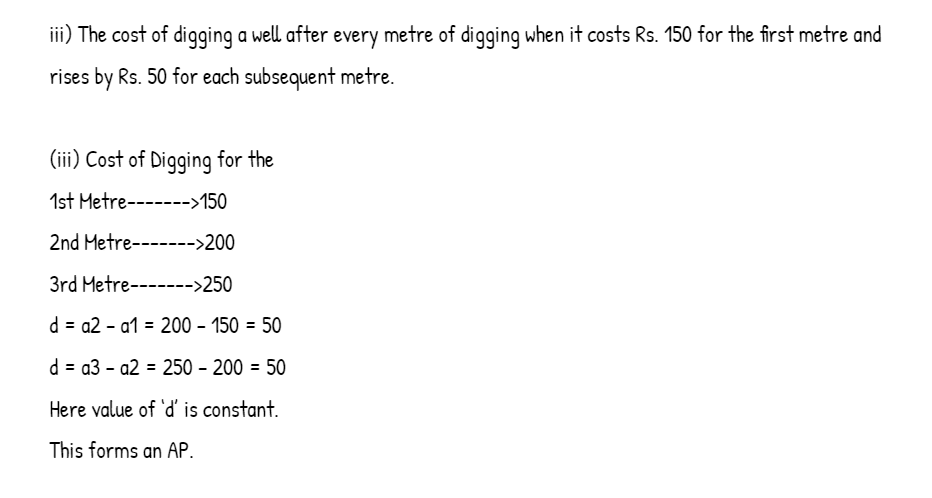
iv) The amount of money in the account every year, when Rs. 10000 is deposited at compound interest at 8% per annum.

Question 2.
Write first four terms of the AP, when the first term ‘a’ and the common difference’d’ are given as follows:
i) a = 10, d = 10
ii) a = -2, d = 0
iii) a = 4, d = -3
iv) a = -1, d = 12
v) a = -1.25, d = 0.25
Solution:
i) a = 10, d = 10
First four terms are,
a, a + d, a + 2d, a + 3d
10, 10 + 10, 10 + 20, 10 + 30
10. 20, 30, 40.

ii) a = -2, d = 0
First four terms are,
a, a + d, a + 2d, a + 3d
-2. -2 + 0, -2 + 0, -2 + 0
-2. -2. -2, -2

iii) a = 4, d = -3
First four terms are,
a, a + d, a + 2d, a + 3d
4, 4 – 3, 4 – 2 × 3, 4 – 3 ×3
4, 1, -2, -5

iv) a = -1, d = 12
First four terms are,
a, a + d, a + 2d, a + 3d
−1,−1+12,−1+2×12,−1+3×12
−1,−12,0,12

v) a = -1.25, d = 0.25
First four terms are,
a, a + d, a + 2d, a + 3d
-1.25, -1.25 + 0.25, -1.25 + 2 × 0.25, -1.25 + 3 ×0.25
-1.25, -1, -0.75, -0.50

Question 3.
For the following APs, write the first term and the common difference :
(i) 3, 1,-1,-3, ………..
(ii) -5, -1, , 7, …………
(iii) 12,12,12,12,……
(iv) 0.6, 1.7, 2.8, 3.9, ………..
Solution:
(i) 3, 1,-1,-3
First term, a = 3,
Common difference, d = a₂ – a₁ = 1 – 3
d = -2.

(ii) -5, -1, 3, 7, ……….
First term, a = -5,
Common difference, d = a₂ – a₁ = -1 – (-5)
d = -1 + 5
d = 4.

(iii) 12,12,12,12,……
First term, a=12
Common difference, d = a₂ – a₁
=12−12
d= 0

iv) 0.6, 1.7, 2.8, 3.9
First term, a = 0.6,
Common difference, d = a₂ – a₁ = 1.7 – 0.6
d= 1.1

Question 4.
Which of the following are APs? If they form an AP, find the common difference ’d’ and write three more terms.
i) 2, 4, 8, 16, …….
ii) 2,52,3,72,……
iii) -1.2, -3.2, -5.2, -7.2
iv) -10, -6, -2, 2, …….
v) 3,3+2–√,3+22–√,3+32–√……
vi) 0.2, 0.22, 0.222, 0.2222, ………
vii) 0, -4, -8, -12, ………
viii) −12,−12,−12,−12,……
ix) 1, 3, 9, 27, ……..
x) a, 2a, 3a, 4a, ………..
xi) a, a², a³, a⁴, ………..
xii) 2–√,8–√,18−−√,32−−√…
xiii) 3–√,6–√,9–√,12−−√
xiv) 1¹, 3², 5², 7²,
xv) 1¹, 5², 7², 73, ……….
Solution:
i) 2, 4, 8, 16…………
d = a₂ – a₁= 4 – 2 = 2
d = a₂ – a₁ = 8 – 4 = 4
Here ‘d’ is not constant.
∴ the given List of numbers does not form an AP.

ii) 2,52,3,72,……
d=a2−a1=52−21=5−42=12
d=a3−a2=31−52=6−52=12
Here ‘d’ is constant.
∴ the given List of numbers form an AP.
Next three terms are: 4,92,5

iii) -1.2, -3.2. -5.2, -7.2
d = a₂ – a₁ = -3.2 – (-1.2) = -3.2+ 1.2
d = -2
d= a₃ – a₂ = -5.2 – (-3.2) = -5.2 + 3.2
d = -2
Here d is constant.
∴ This is an Arithmetic Progression.
Next three terms are:
-7.2 – 2 = -9.2
-9.2 – 2 = -11.2
-11.2 – 2 = -13.2
-11.2-2 = -13.2

iv) -10. -6. -2, 2,..,…
d = a₂ – a₁ = -6 – (- 10) = -6 + 10
d = 4
d = a₃ – a₂= -2 – (-6) = -2 + 6
d = 4
Here d is constant.
∴ Given set of numbers form an A.P.
Further three terms are
2 + 4 = 6
4 + 4 = 8
8 + 4 = 12

v) 3,3+2–√,3+22–√,3+32–√……
d = a₂ – a₁ = =3+2–√−3
d=2–√
d = a₃ – a₂ = =3+22–√−(3+2–√)
=3+22–√−3+2–√
d=2–√
Here ‘d’ is constant
∴ Given set of numbers forms an A.P.
Further three terms are:
3+32–√+2–√=3+42–√
3+42–√+2–√=3+52–√
3+52–√+2–√=3+62–√

vi) 0.2. 0.22. 0.222. 0.2222
d = a₂ – a₁ = 0.22 – 0.2
d = 0.02
d = a₃ – a₂ = 0.222 – 0.22
d = 0.002
Here d is not constant,
∴ Given set of numbers do not form an A.P.

vii) 0,-4, -8, -12, …………
a₁ = 0, a₂ = -4
d = a₂ – a₁ = -4 – 0
d = -4
d = a₃ – a₂ = -8 – (-4) = -8 + 4
d = -4
Here d is constant.
∴ Given set of numbers form an AP.
Further three terms are:
-12 – 4 = -16
-16 – 4 = -20
-20 – 4 = -24
∴ Next three terms are: -16. -20, -24.

viii) −12,−12,−12,−12,……
a1=−12,a2=−12
d=a2−a1=−12−(−12)
d=−12+12=0
d=a3−a2=−12−(−12)
d=−12+12=0
Here d is constant.
∴ Given set of numbers form an AP.
Next three terms are:
−12+0=−12
−12+0=−12
−12+0=−12
∴ Next three terms are: −12,−12,−12

ix) 1, 3, 9, 27
d = a₂ – a₁ = 3—1
d = 2
d = a₃ – a₂
d = 6
Here ‘d’ not is constant
∴ Given set of numbers do not form an A.P.

x) a, 2a, 3a,4a
a₁= a a₂ = 2a
d = a₂ – a₁ = 2a-a
d = a
d = a₃ – a₂ = 3a-2a
d = a
Here d’ is constant.
∴ Given set of numbers form an A.P.
Further three terms are :
4a + a = 5a
5a + a = 6a
6a + a = 7a
∴ Next three terms are: 5a, 6a, 7a.

xi) a, a², a³, a⁴
a₁ = a. a₂ = a²
d = a₂ – a₁ = a² – a
d= a(a – 1)
d = a₃ – a₂ = a³ – a²
d = a² (a – 1)
Here ‘d is not constant.
∴ Given set of numbers do not form an A.P.

xii) 2–√,8–√,18−−√,32−−√…
a1=2–√,a2=8–√
d=a2−a1=8–√−2–√
d=22–√−2–√=2–√
d=a3−a2=18−−√−8–√
d=32–√−22–√=2–√
Here d’ is constant.
∴ Given set of numbers form an A.P.
Succeding three terms are :
32−−√+2–√=42–√+2–√=52–√
52–√+2–√=62–√
62–√+2–√=72–√
52–√,62–√,72–√
∴ Next three terms are: 50−−√,72−−√,98−−√

xiii) 3–√,6–√,9–√,12−−√
a1=3–√,a2=6–√
d=a2−a1=6–√−3–√
d=a3−a2=9–√−6–√
d=3−6–√
Here ‘d is not constant.
∴ Given set of numbers do not form an A.P.

xiv) 1¹,3²,5², 7², …………
1, 9, 25, 49, ………….
a₁ = 1, a₂ = 9
d = a₂ – a₁ = 9 – 1
d = 8
d = a₃ – a₂ = 25 – 9
d = 16
Here ‘d’ is not constant,
∴ Given set of numbers do not form an A.P.

xv) 1¹, 5², 7², 73, ……….
1, 25. 49, 73, ……….
a₁ = 1. a₂ = 25, a₃ = 49, a₄ = 73
d = a₂ – a₁ = 25 – 1
d = 24
d = a₃ – a₂ = 49 – 25
d = 24
d = a₄ – a₃ = 73 – 49
d = 24
Here ‘d’ is constant.
∴ Given set of numbers form an A.P.
Succeeding three terms are:
73 + 24 = 97
97 + 24 = 121
121 + 24 = 145
∴ Next three terms are: 97, 121, 145.

We hope the given KSEEB SSLC Class 10 Maths Solutions Chapter 1 Arithmetic Progressions Ex 1.1 will help you. If you have any query regarding Karnataka SSLC Class 10 Maths Solutions Chapter 1 Arithmetic Progressions Exercise 1.1, drop a comment below and we will get back to you at the earliest.Categories