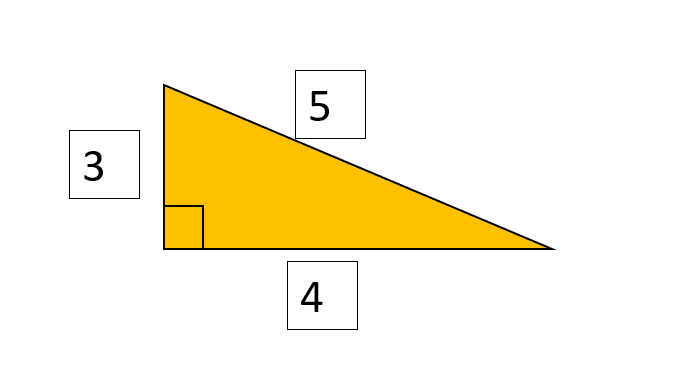
Three positive numbers a, b, and c make up a Pythagorean triple if their sum, a2 + b2, equals their sum, c2. A standard way to write such a triple is (a, b, c). One of the most common well-known example of Pythagorean triples is (3, 4, 5).
Complete List of Pythagorean Triples
Pythagorean triples are formed by positive integers a, b and c, such that a2 + b2 = c2. We may write the triple as (a, b, c).
For example, the numbers 3, 4 and 5 form a Pythagorean Triple because 32 + 42 = 52. There are infinitely many Pythagorean triples.
Some most commonly used triplets are:
| a | b | c |
|---|---|---|
| 3 | 4 | 5 |
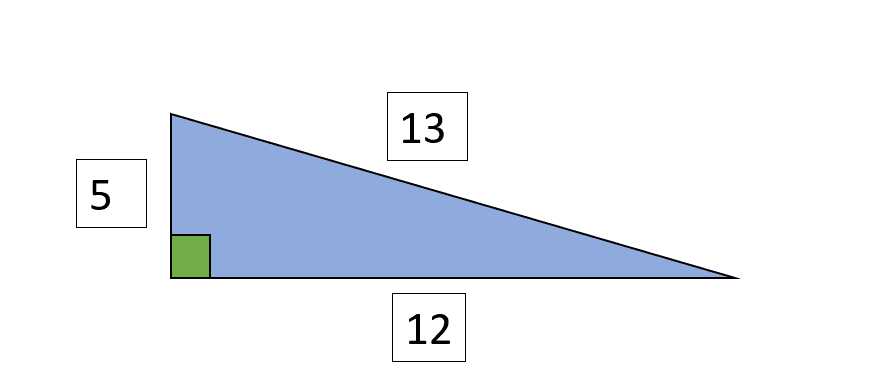
| 5 | 12 | 13 |
| 6 | 8 | 10 |
| 7 | 24 | 25 |
| 8 | 15 | 17 |
| 9 | 40 | 41 |
| 10 | 24 | 26 |
| 11 | 60 | 61 |
| 12 | 35 | 37 |
| 13 | 84 | 85 |
| 15 | 112 | 113 |
| 16 | 63 | 65 |
| 18 | 24 | 30 |
| 17 | 144 | 145 |
| 19 | 180 | 181 |
| 20 | 21 | 29 |
| 20 | 99 | 101 |
| 21 | 220 | 221 |
| 28 | 45 | 53 |
| 36 | 77 | 85 |
| 39 | 80 | 89 |
| 65 | 72 | 97 |
Pythagoras Theorem Examples and Questions
Example 1: ∆ ABC is right-angled at C. If AC = 5 cm and BC = 12 cm find the length of AB.
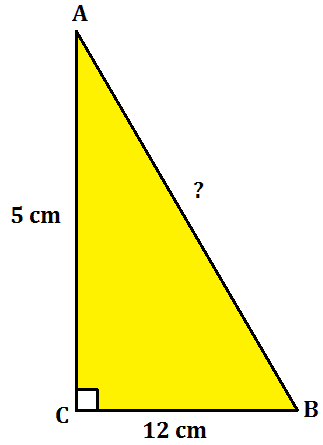
Refer to the figure given on the right.
As the triangle is right-angled, by Pythagoras theorem,
AB² = AC² + BC²
AB² = 5² + 12²
AB² = 25 + 144
AB² = 169 = 13²
Hence, AB = 13 cm
Example 2 : The side of a square is given to be 4 cm. Find the length of the diagonal of a square.
Solution: We need to find the length of the diagonal AC. As we know, all sides of a square are equal and each angle is 90 degrees, ADC is a right-angled triangle.
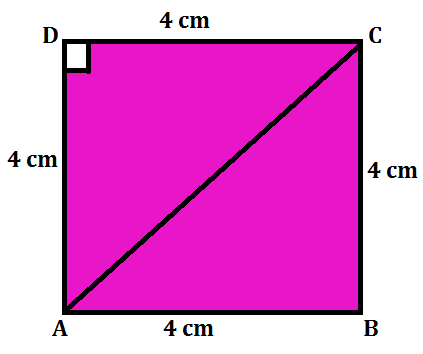
By Pythagoras theoram,
AD² + CD² = AC²
AC² = 4² + 4² = 16 + 16
AC² = 32, So, AC= 4√2
The diagonal of the square is 4√2 cm.