NCERT Class 9 Maths Solutions PDF: In this post, we have discussed the solution of the Maths Class 9 book Chapter 8. Solutions are given below with proper explanation and utmost care has been taken to ensure that the solutions are correct. The answers provided will not only help in completing all the assignments but also help students in clearing their concepts. Students can download the solutions by printing the chapters by using the command Ctrl+P in Google Chrome and saving it in PDF format. All the best !! Please support us by sharing this website with your school friends.
Exercise 8.1 Class 9 Maths Chapter 8 Quadrilaterals Solutions
1. The angles of quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the quadrilateral.

2. If the diagonals of a parallelogram are equal, then show that it is a rectangle.

3. Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.

4. Show that the diagonals of a square are equal and bisect each other at right angles.


5. Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.

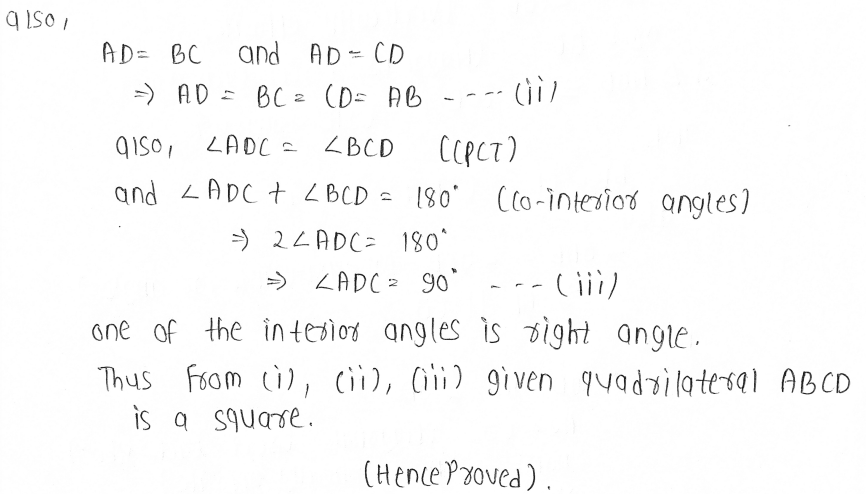
6. Diagonal AC of a parallelogram ABCD bisects ∠ A (see Fig. 8.19). Show that
(i) it bisects ∠ C also,
(ii) ABCD is a rhombus.
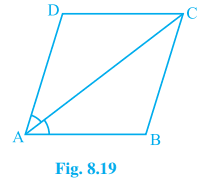

7. ABCD is a rhombus. Show that diagonal AC bisects ∠ A as well as ∠ C and diagonal BD bisects ∠ B as well as ∠ D.

8. ABCD is a rectangle in which diagonal AC bisects ∠ A as well as ∠ C. Show that:
(i) ABCD is a square (ii) diagonal BD bisects ∠ B as well as ∠ D.
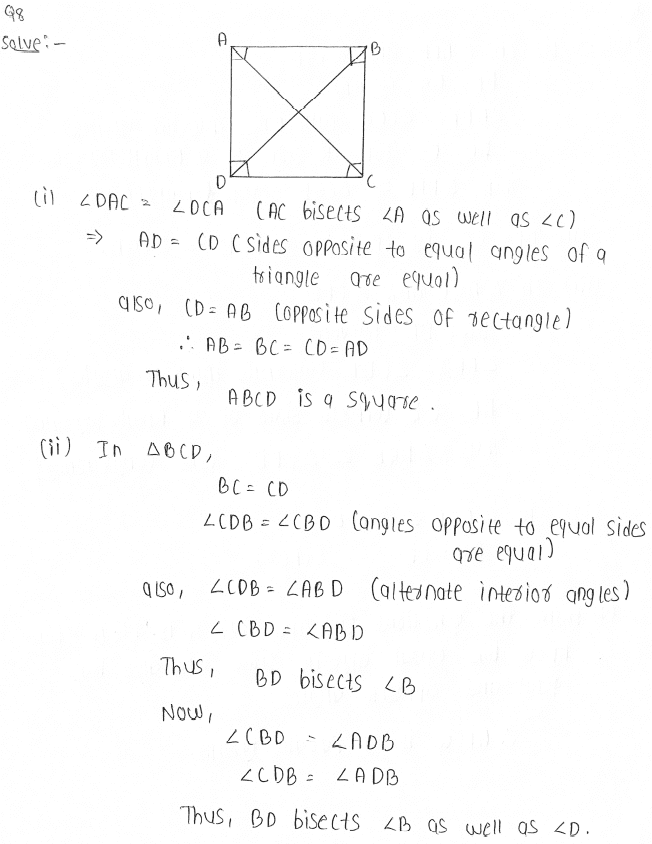
9. In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig. 8.20). Show that:
(i) ∆ APD ≅ ∆ CQB
(ii) AP = CQ
(iii) ∆ AQB ≅∆ CPD
(iv) AQ = CP
(v) APCQ is a parallelogram
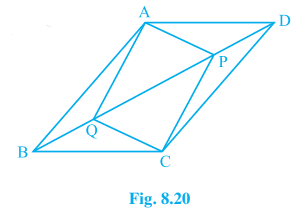

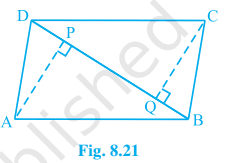
10. ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (see Fig. 8.21). Show that
(i) ∆ APB ≅ ∆ CQD
(ii) AP = CQ
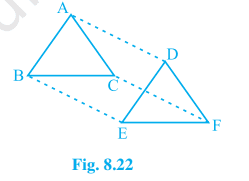
11. In ∆ ABC and ∆ DEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, B and C are joined to vertices D, E and F respectively (see Fig. 8.22). Show that
(i) quadrilateral ABED is a parallelogram
(ii) quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ∆ ABC ≅ ∆ DEF.

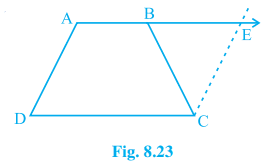
12. ABCD is a trapezium in which AB || CD and AD = BC (see Fig. 8.23). Show that
(i) ∠ A = ∠ B
(ii) ∠ C = ∠ D
(iii) ∆ ABC ≅ ∆ BAD
(iv) diagonal AC = diagonal BD
[Hint : Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]
![Exercise 8.1 Class 9 Maths Chapter 8 Quadrilaterals ABCD is a trapezium in which AB || CD and AD = BC (see Fig. 8.23). Show that
(i) ∠ A = ∠ B
(ii) ∠ C = ∠ D
(iii) ∆ ABC ≅ ∆ BAD
(iv) diagonal AC = diagonal BD
[Hint : Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]](https://ncertbookspdf.com/wp-content/uploads/2022/04/image-318.png)
1 thought on “Exercise 8.1 Class 9 Maths Chapter 8 Quadrilaterals”